Trusted by 12,000+ innovators worldwide


Eliminate friction from your workflows
Patsnap saves you valuable time and resources with a connected product suite.
- FOR R&D
- FOR IP
-
IDEATE
-
VALIDATE
-
REVIEW
-
SUBMIT
-
MONITOR
- Idea
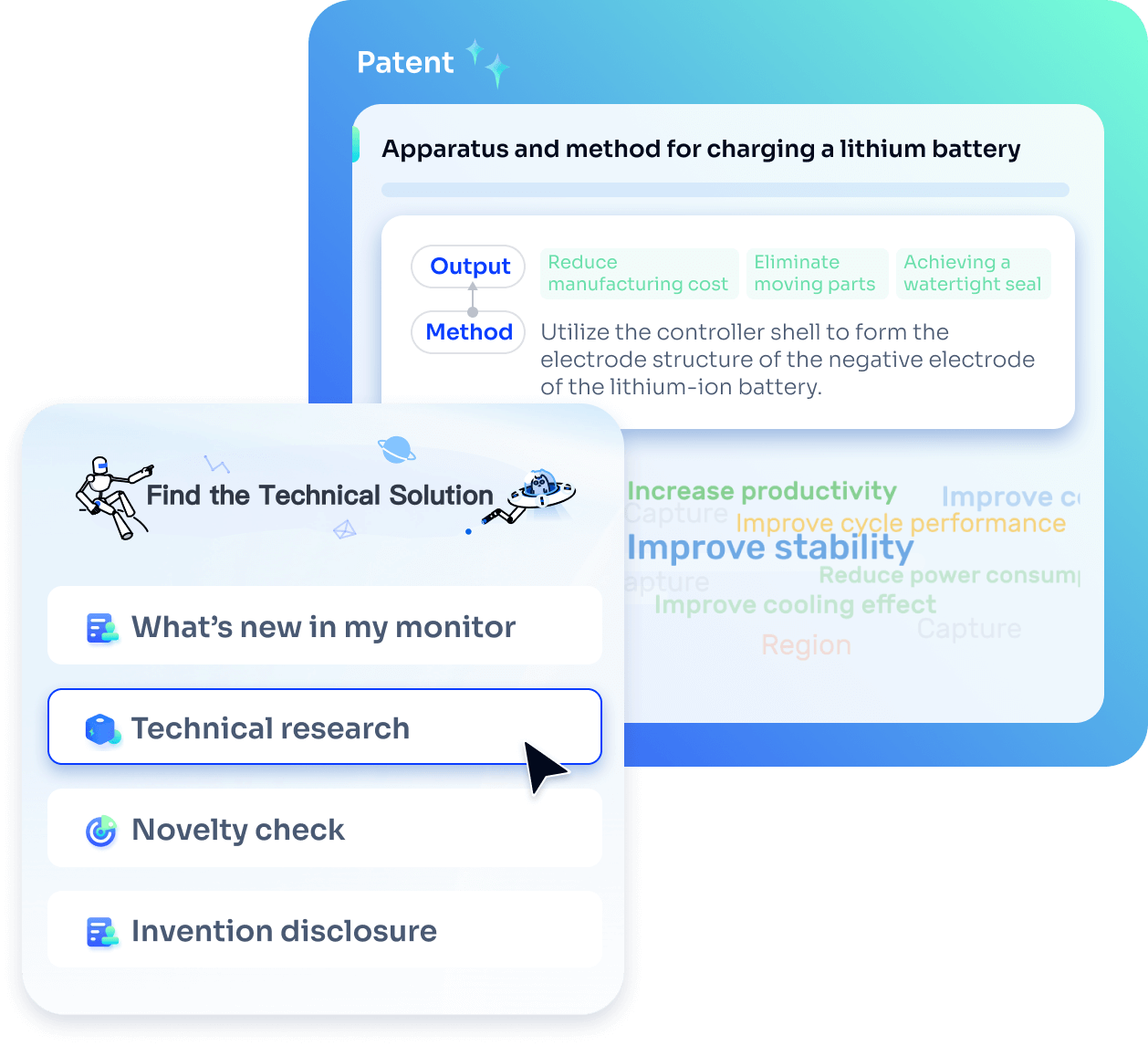
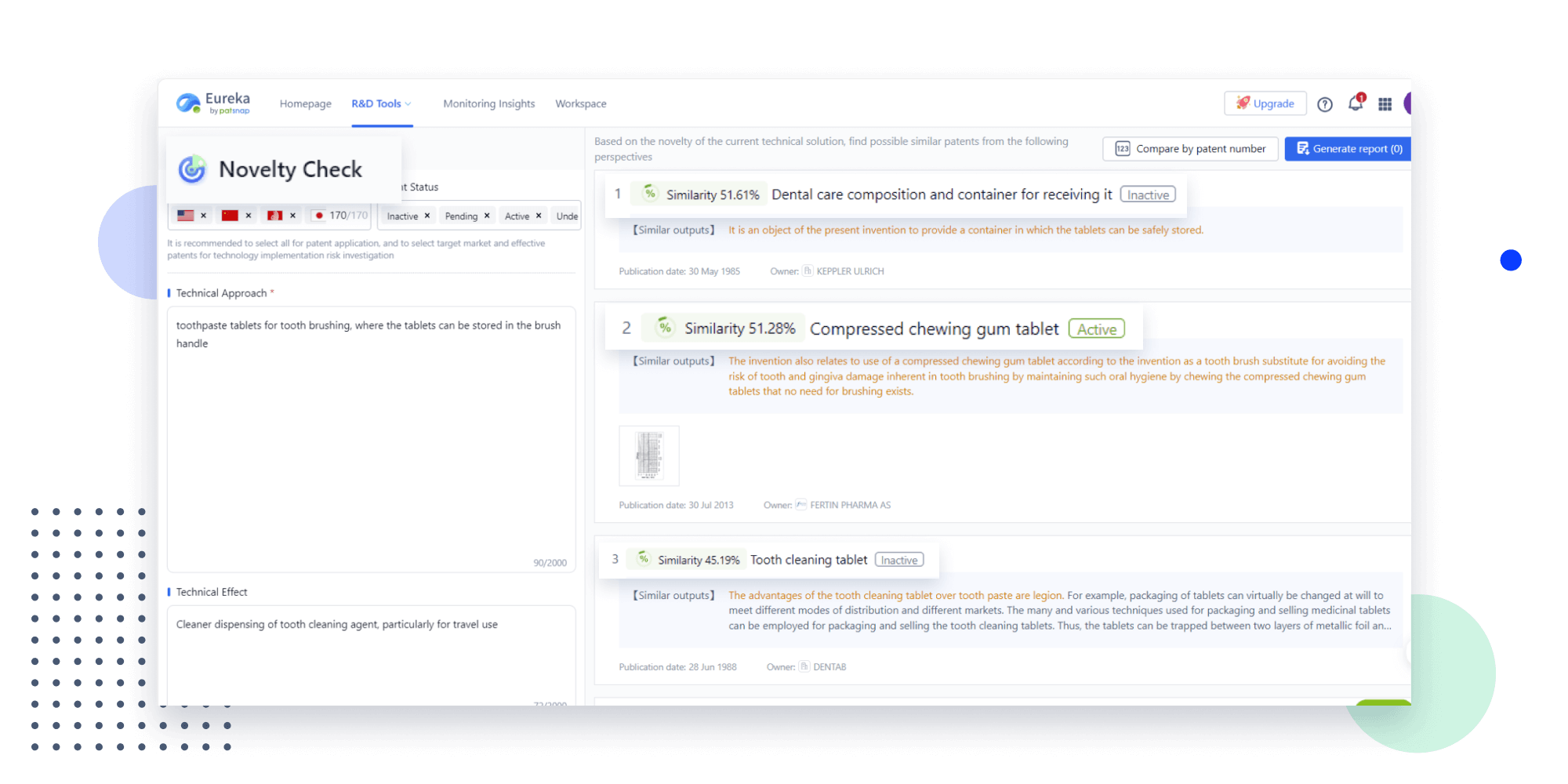
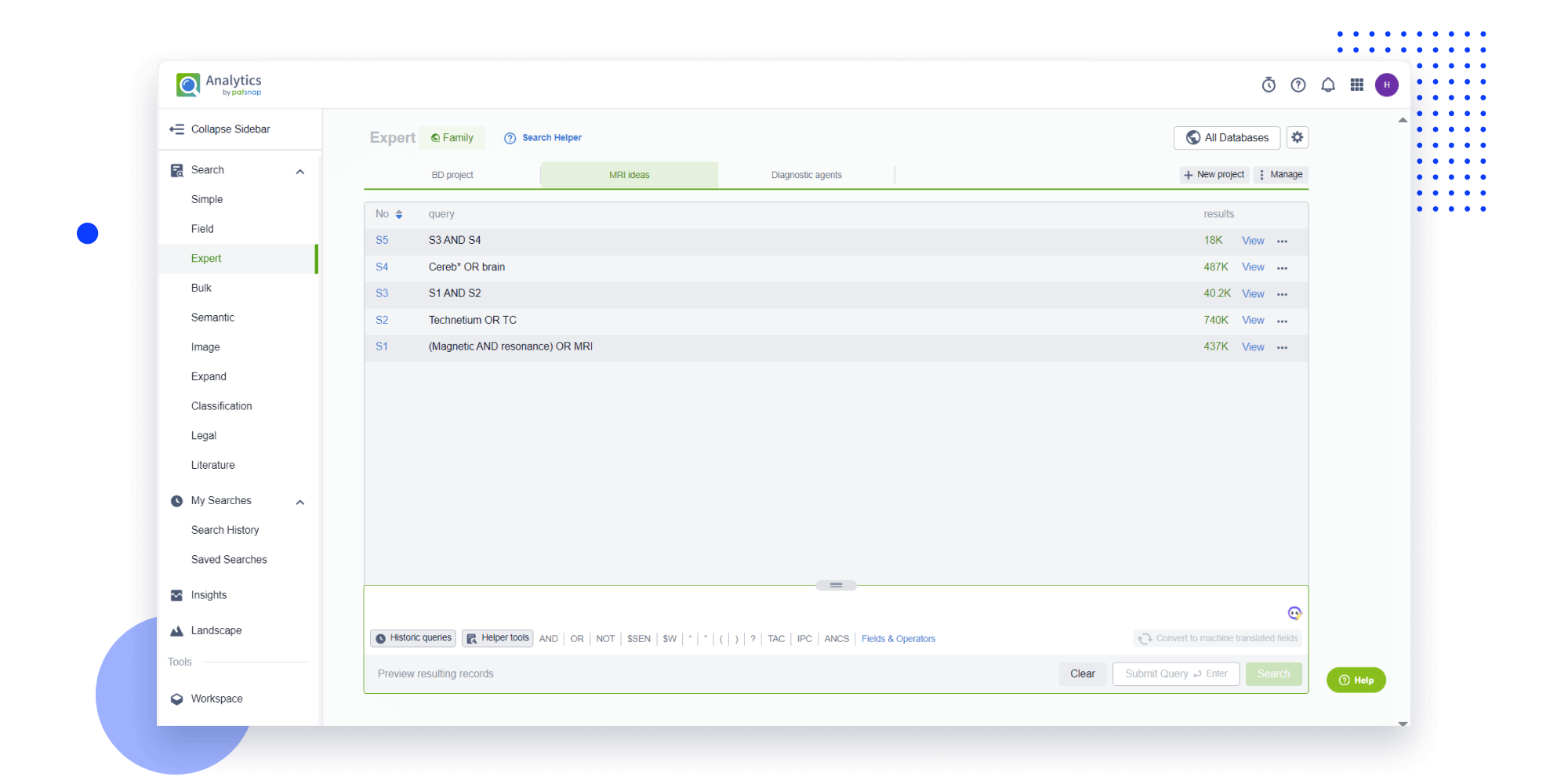
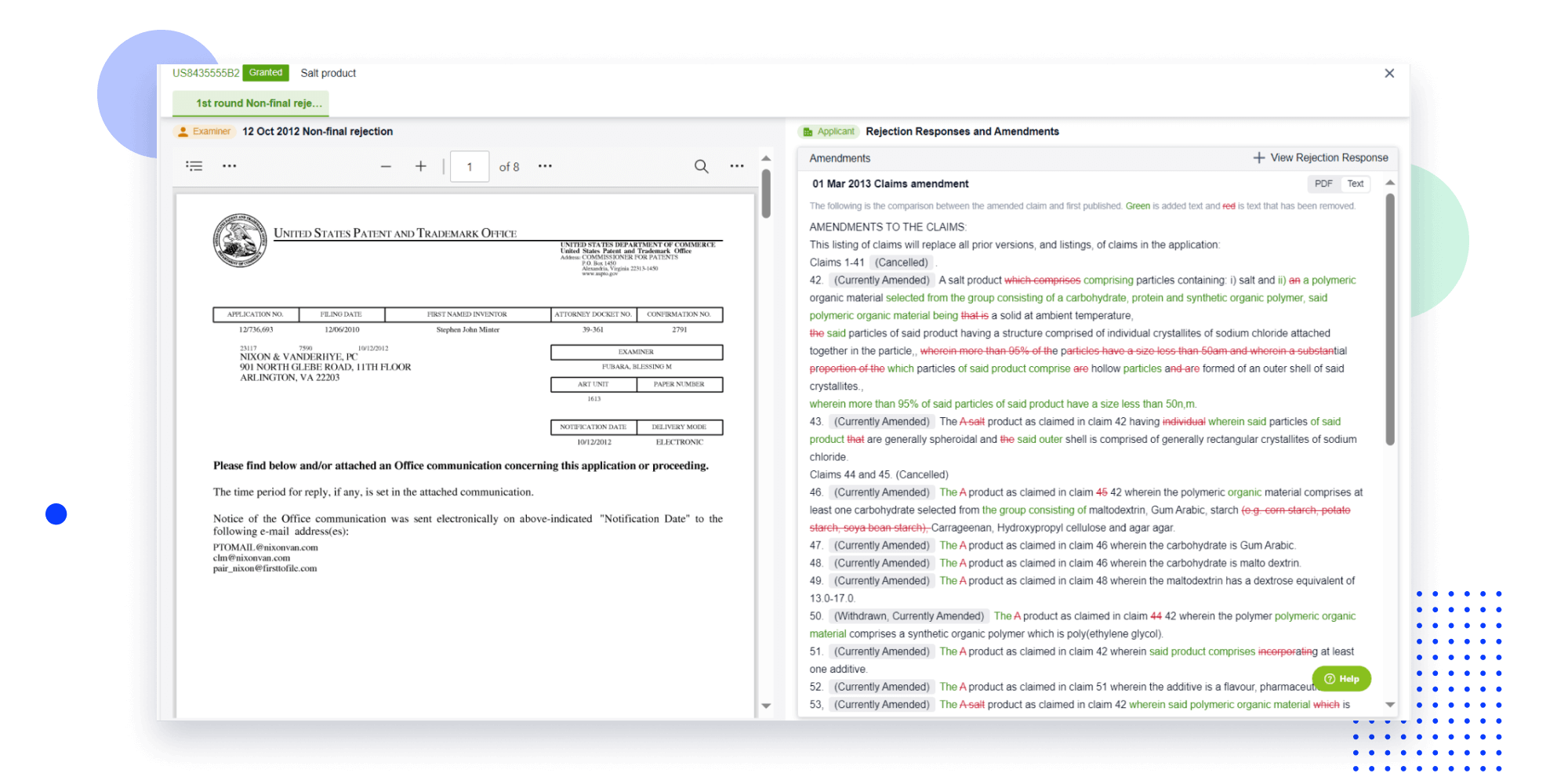
Strengthen FTO and prior art search with AI tools, collaboration, and global data
Write your product, invention idea, or a patent of interest’s publication number and search over 180+ million patents and 130+ million pieces of literature from 170 jurisdictions.
Explore Analytics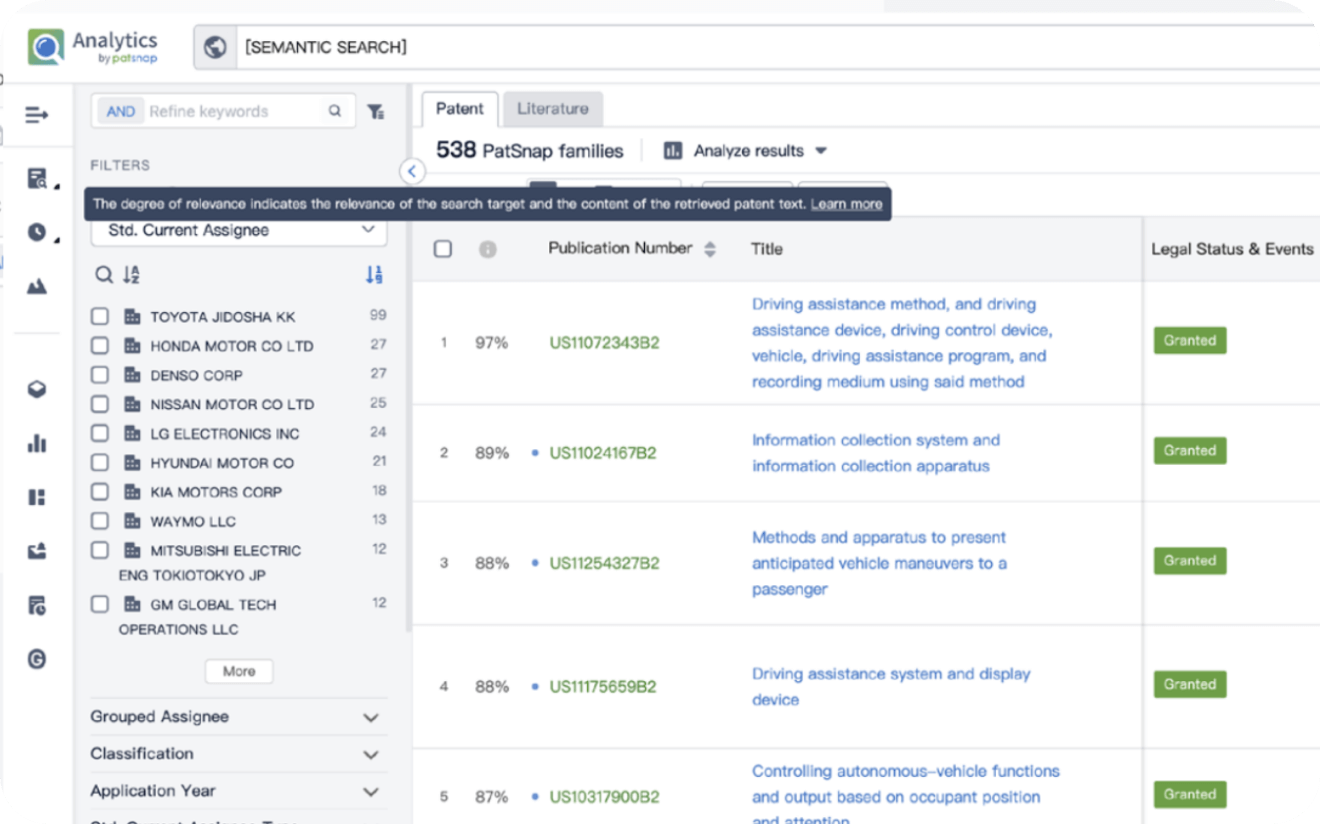
- Refinement
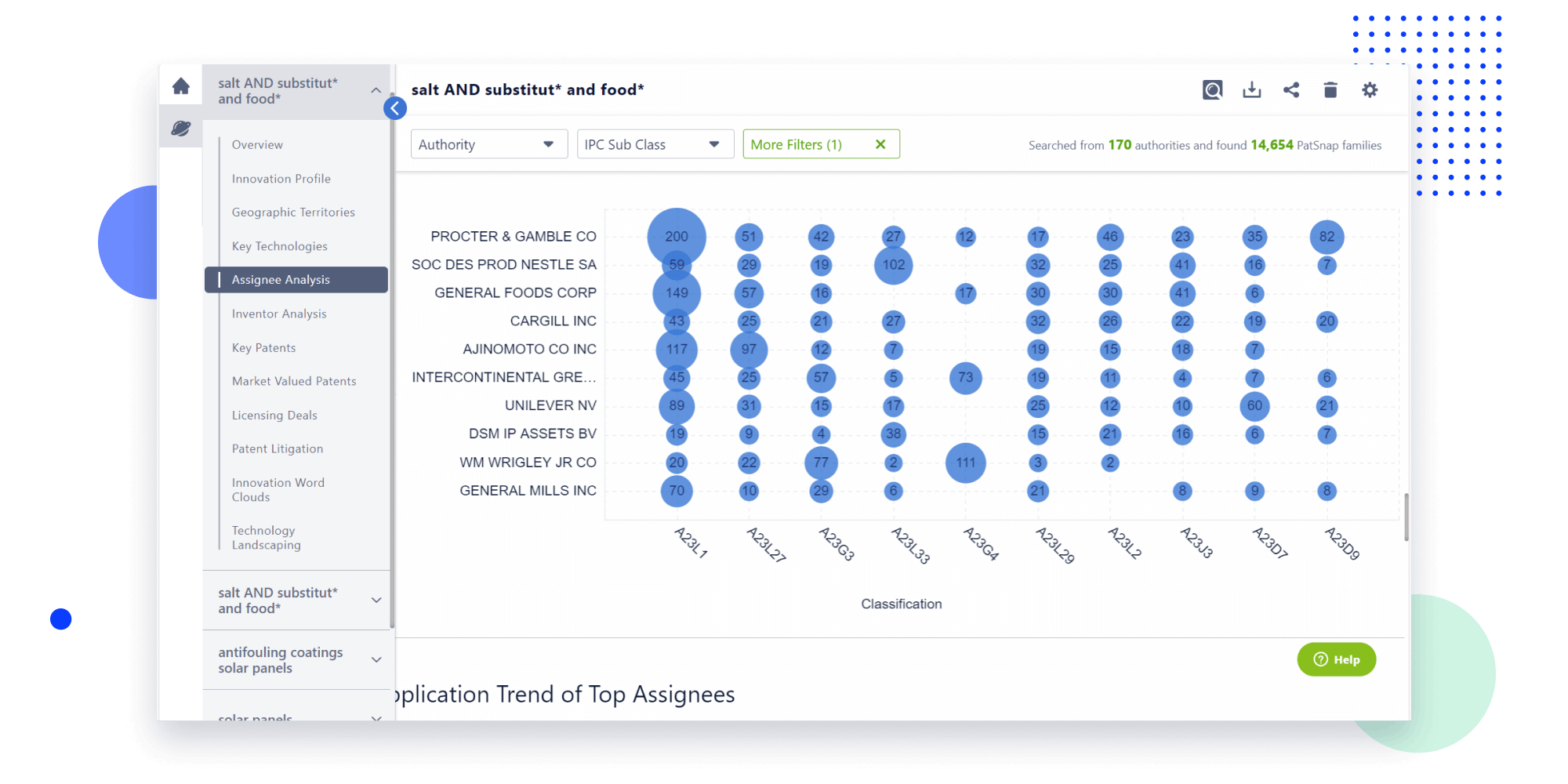
Narrow your search to what you need, automatically with AI
Patsnap’s Keyword Helper auto-generates the correct code for complex queries. Search by bulk, classification, image, and chemical in a snap.
Explore Eureka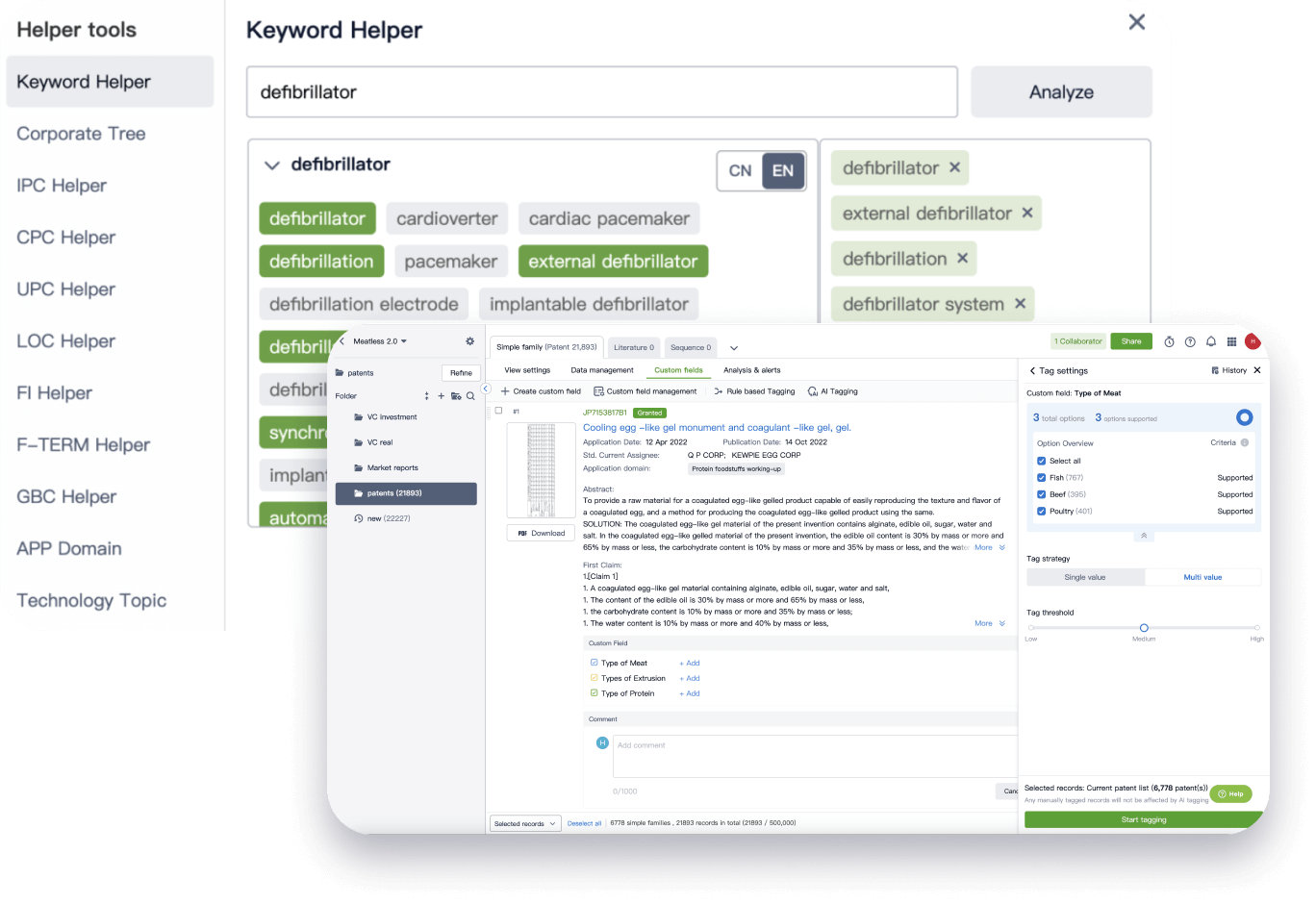
- Insight
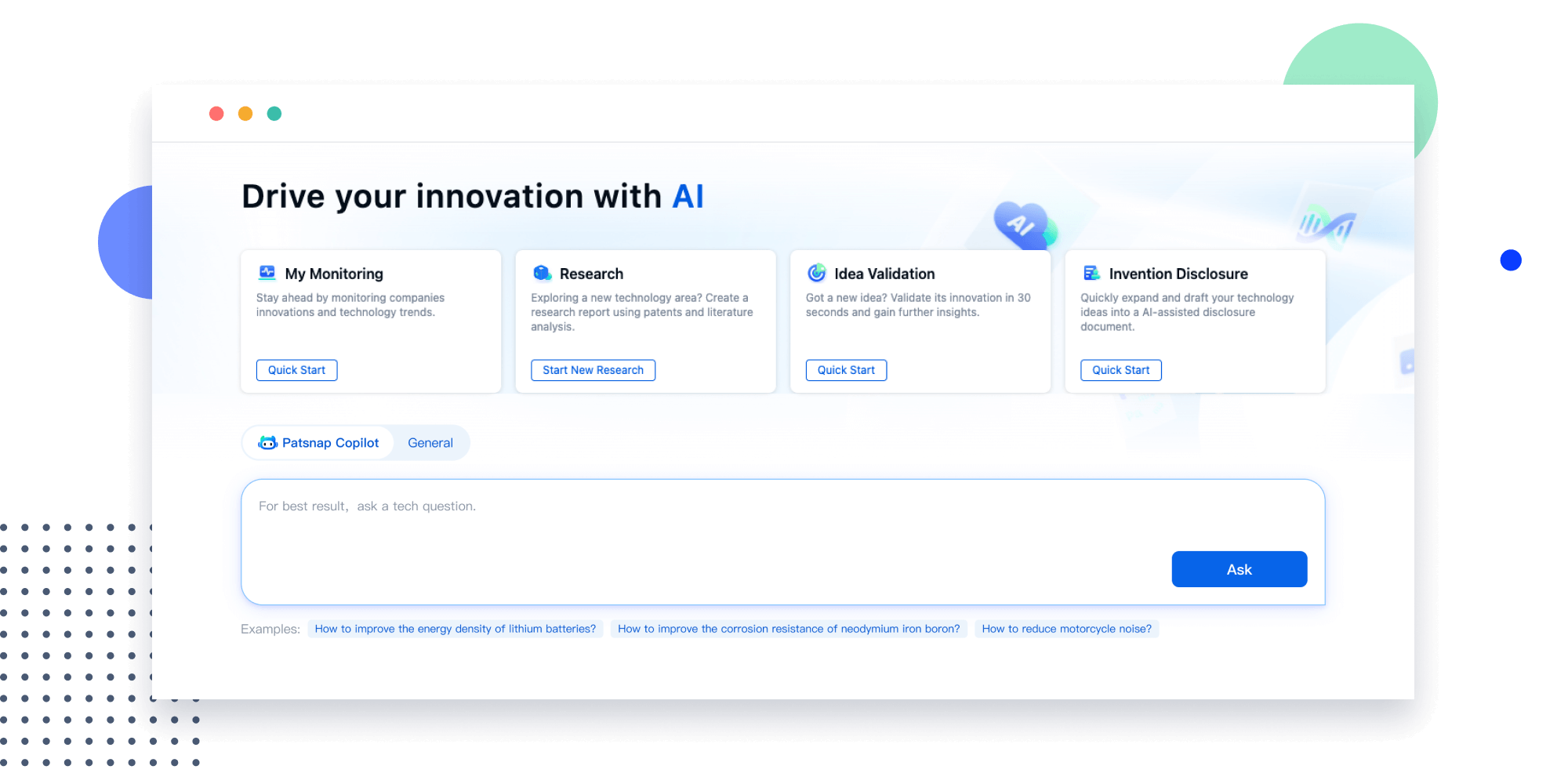
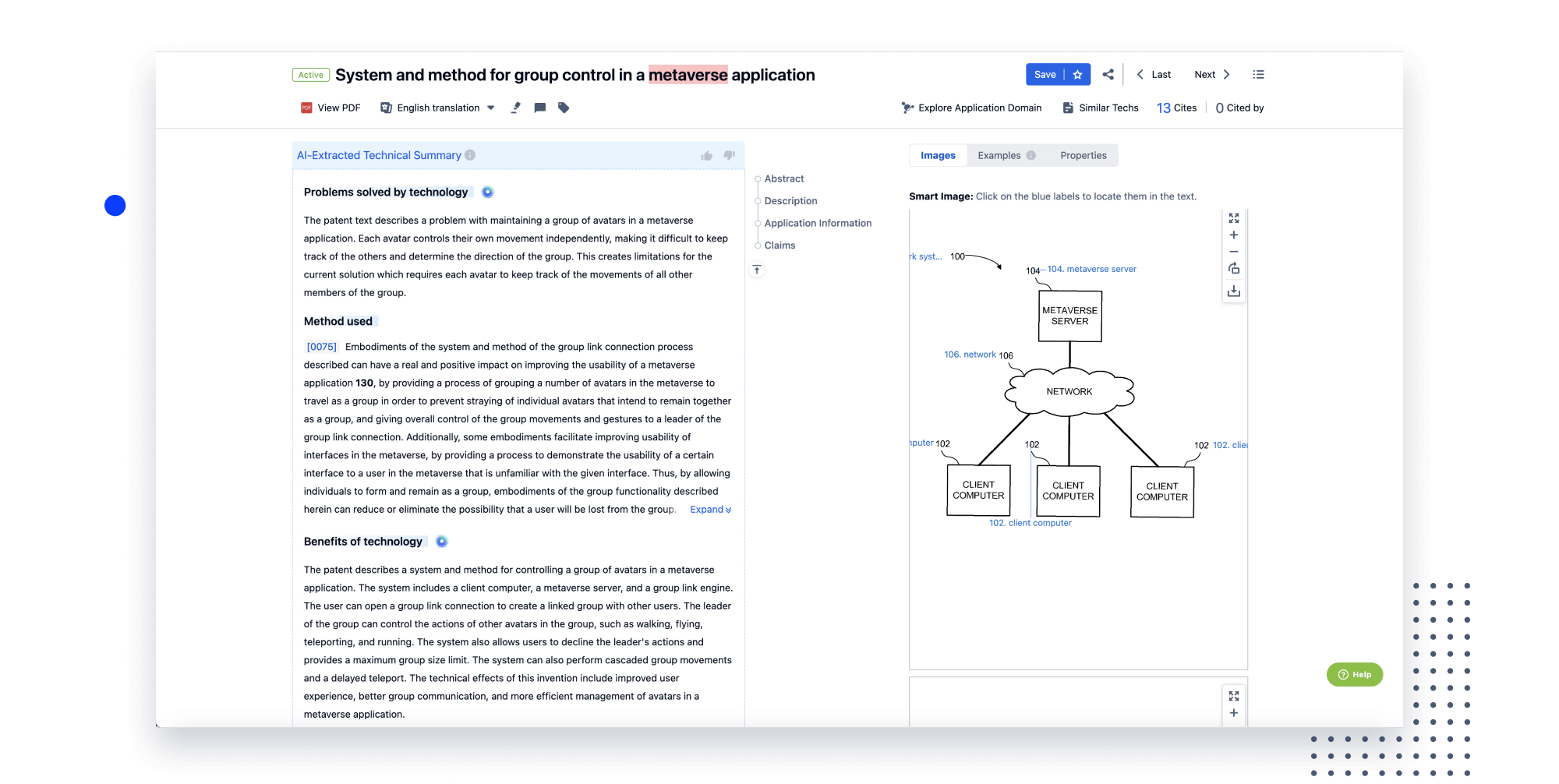
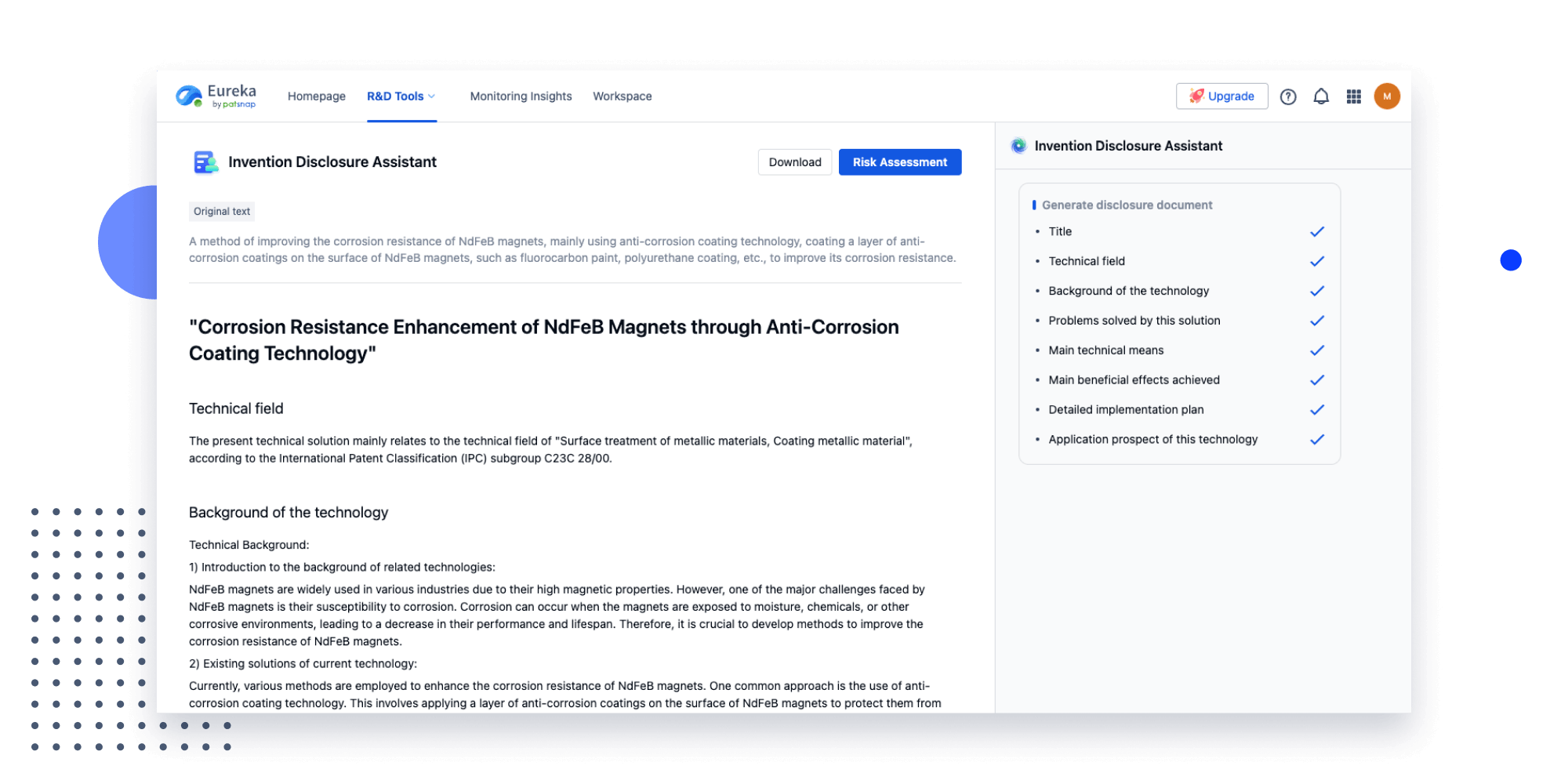
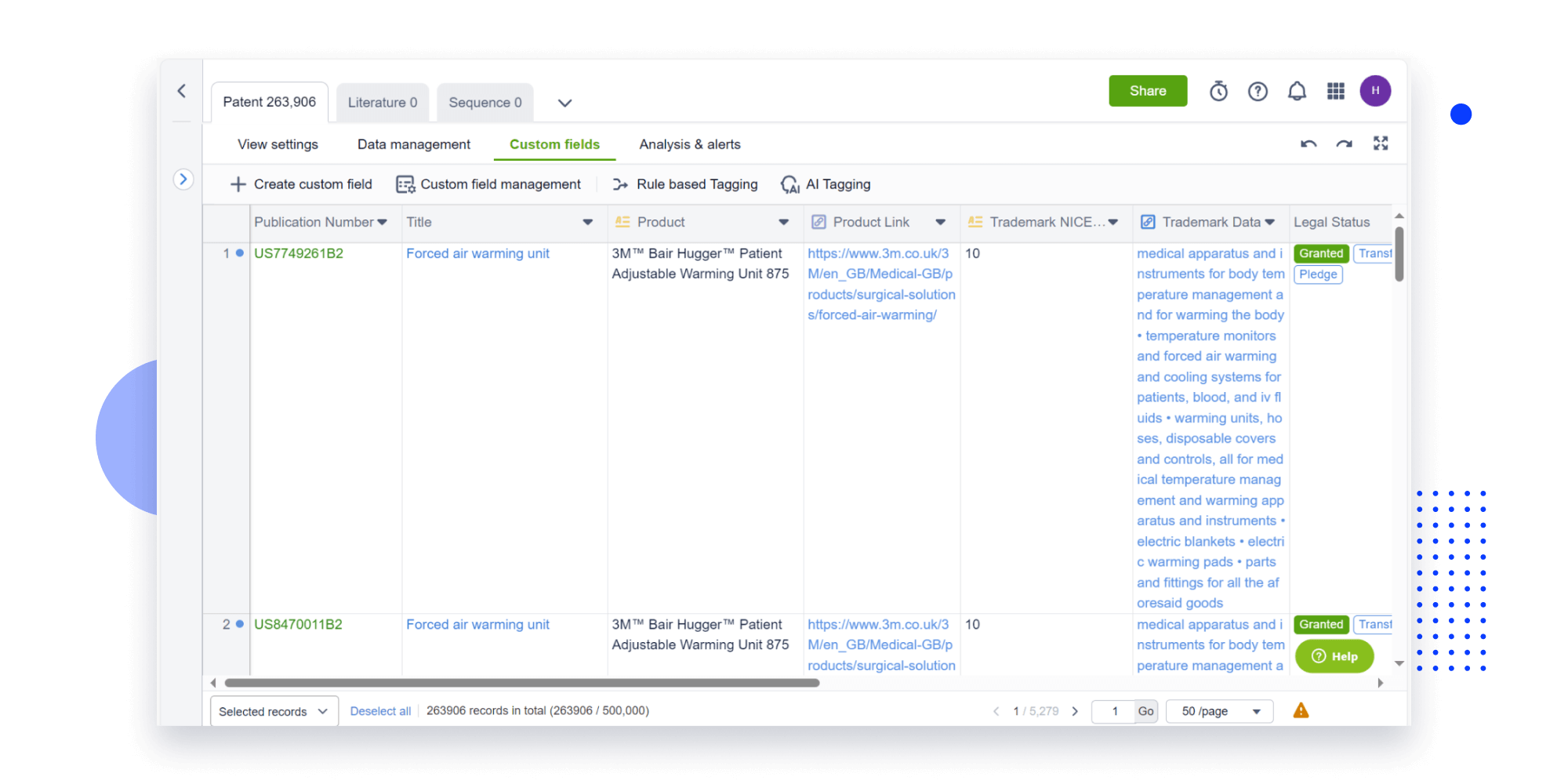
Extract key info, risks, and opportunities with a single click
PatentDNA decodes technical information, making it easy to find similar technologies, citations, images, and more. All with their precise references in the patent.
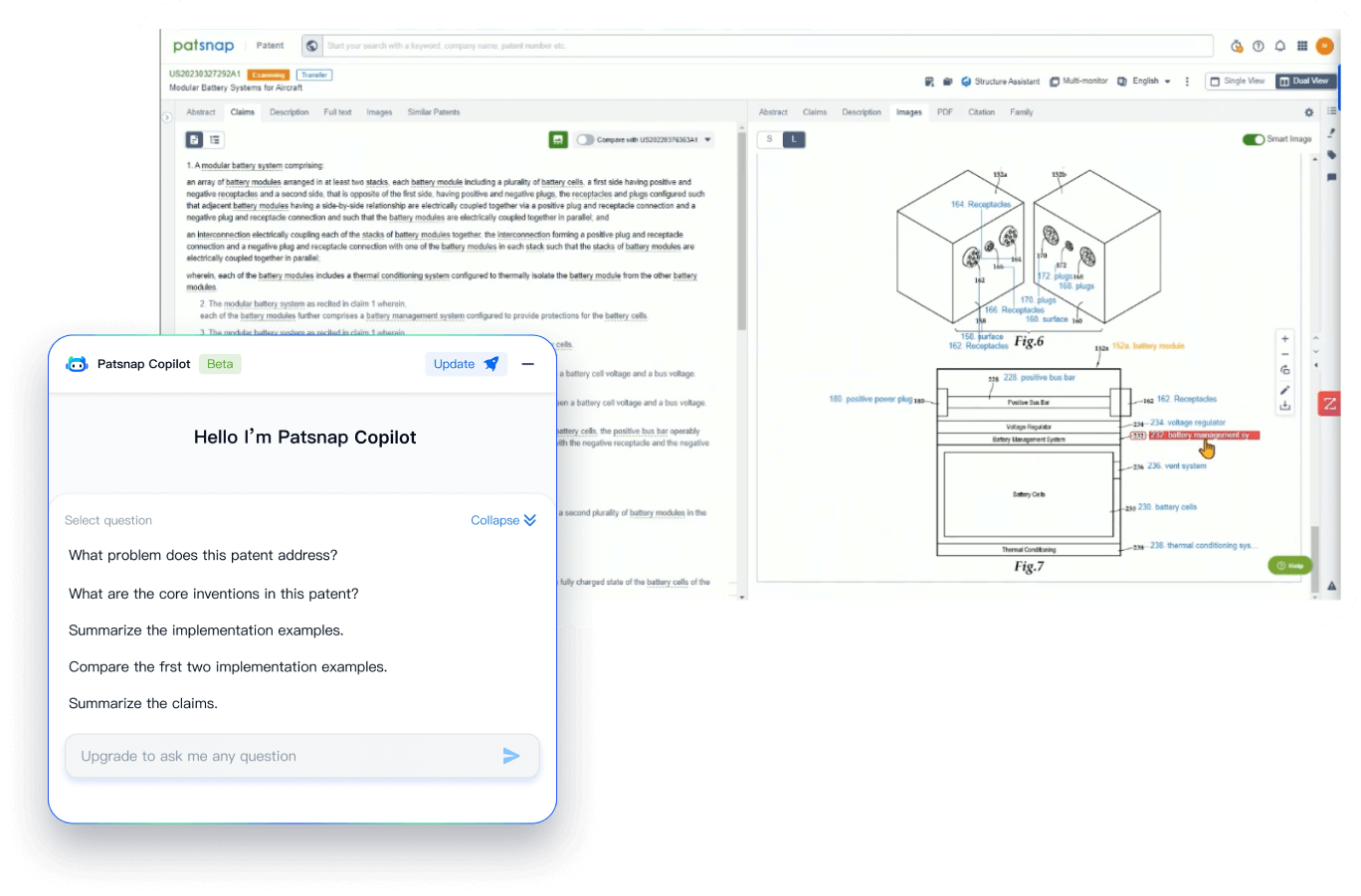
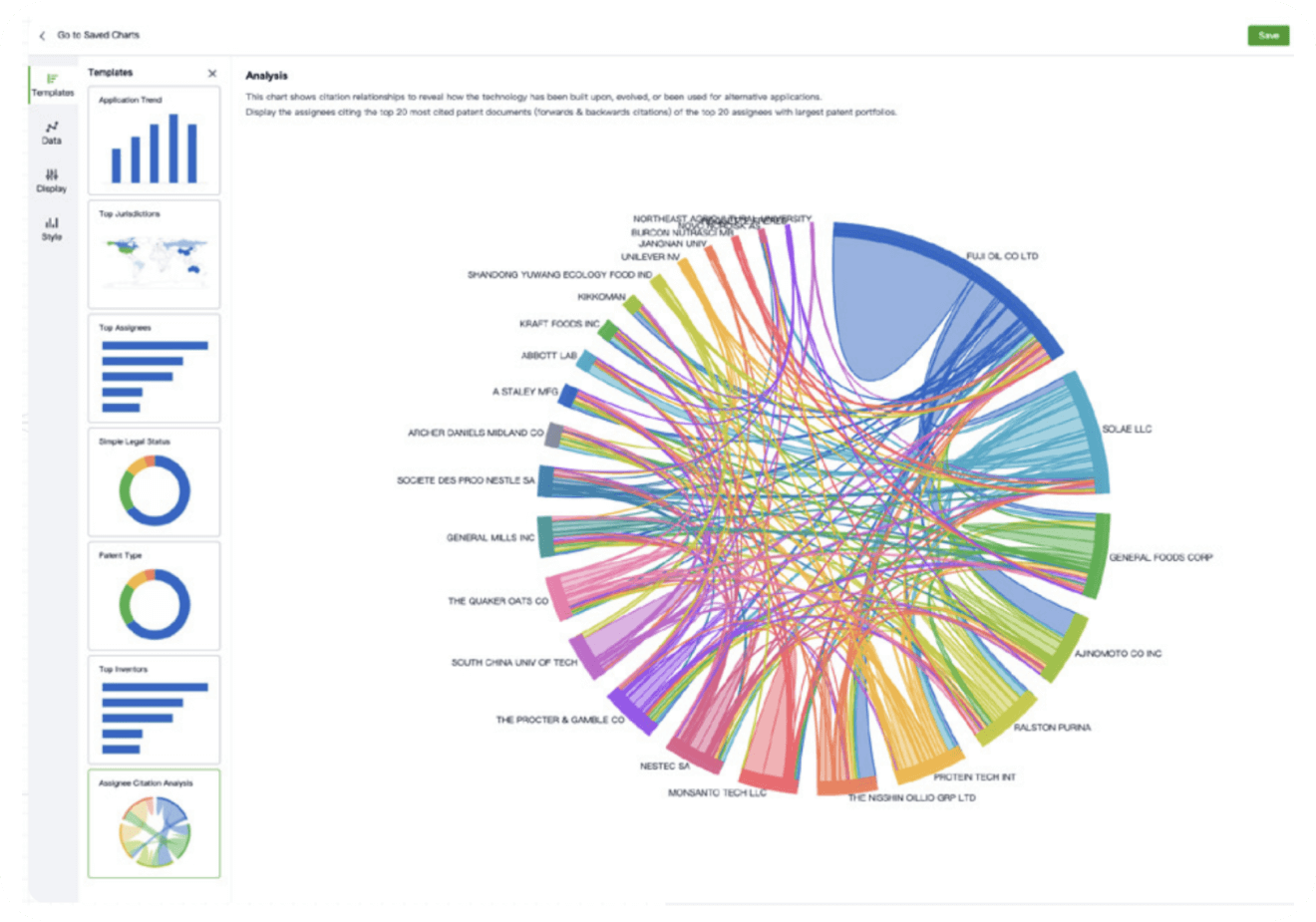
- Analysis
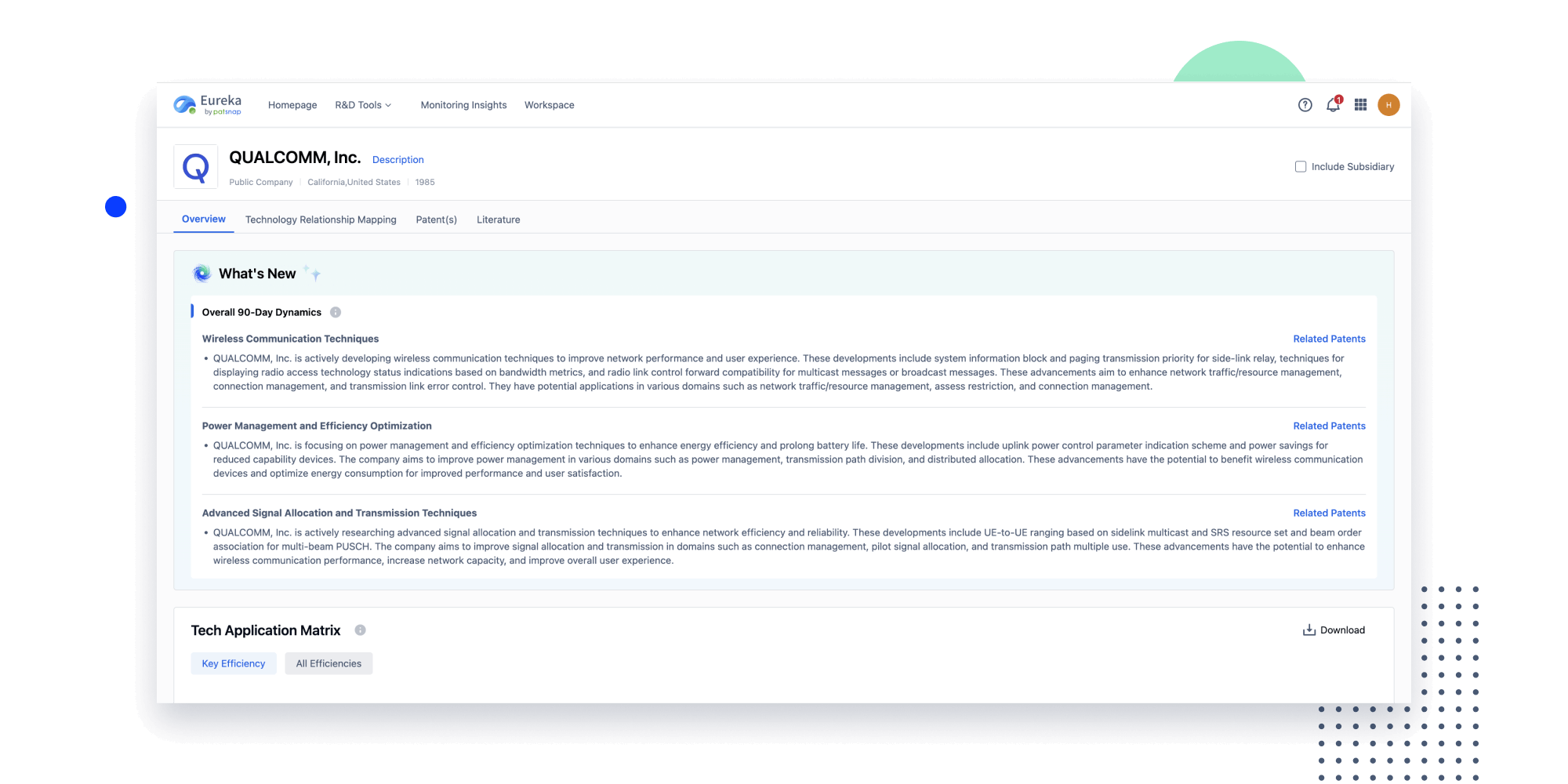
Instantly turn IP research into a competitive advantage
Patsnap’s proprietary AI applies machine learning and natural language processing to auto-generate keywords, so you can quickly understand the invention technology in a patent.
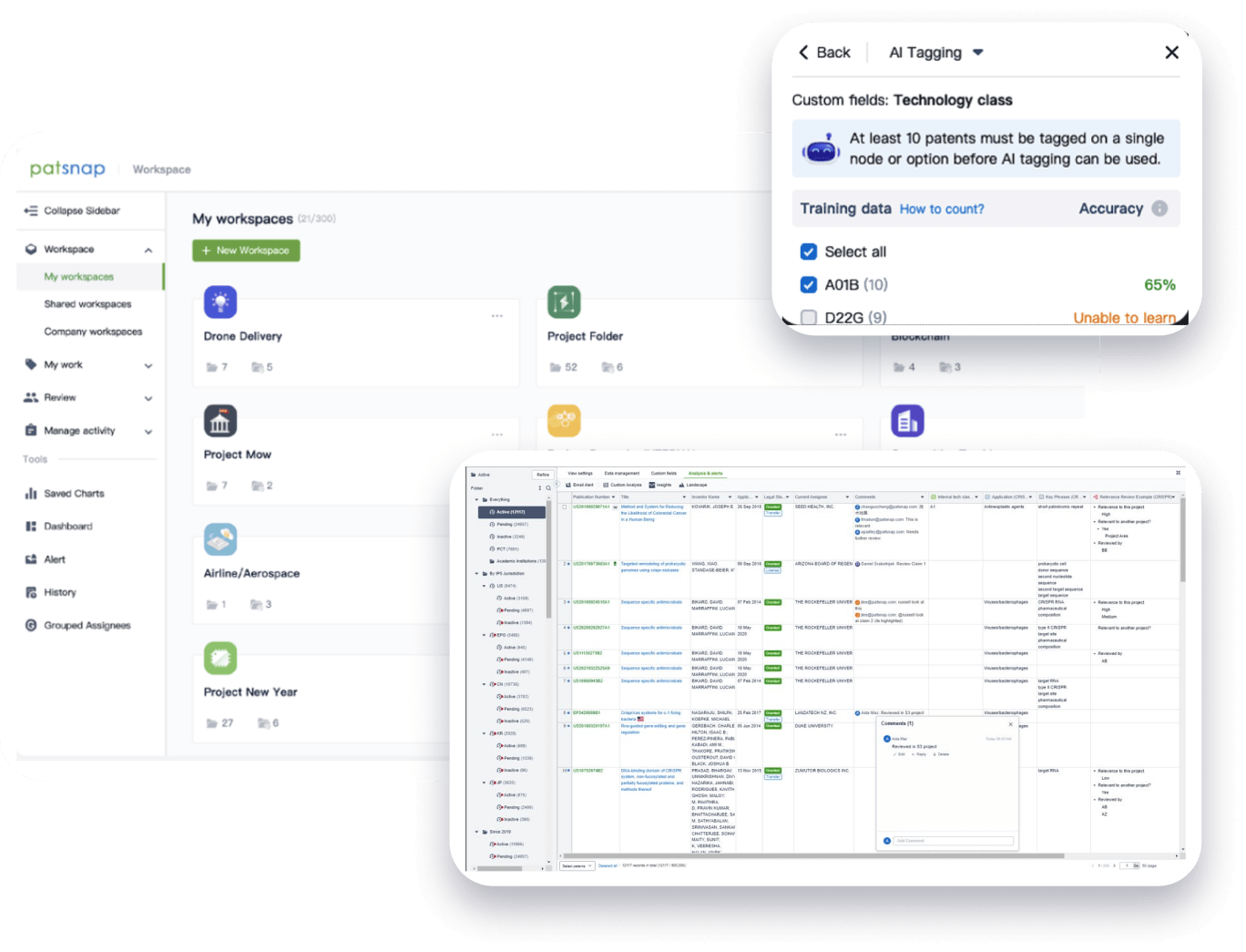
- Collaboration
Speed up decisions with an intuitive workspace
Add comments, tag teammates, and categorize patents with AI tagging. Keep a pulse on competitors via automated notifications.
From startups to Fortune 500s,
the world’s most innovative teams trust Patsnap.
-
Using Patsnap has led to tremendous acceleration — over 100% — of our technology assessment and scouting processes.
Antonio Batistini
Chief Technology Innovation Officer -
Patsnap's interface is extraordinarily intuitive and versatile. What really sets Patsnap apart is the customer support. They really feel like part of our team.
Tycho Speaker
President -
Patsnap makes patent data insightful and helps us identify the white space to innovate in. It gives our team the best chance of success.
Caroline Priestley
Head of IP
Built for enterprise scale and security
-
170
Jurisdictions
-
188M
Patents
-
132M
Literature
-
Secure, proprietary AI
Prioritizing data confidentiality, Patsnap AI is trained exclusively on patent-related data and never on customer data.
-
ISO 27001 certification
As part of our adherence to ISO 27001, we undergo annual 3rd party audits to ensure your data is safe and secure.
-
Data protection
Patsnap is committed to protecting customer data and enhance practices to comply with GDPR, CCPA, and CPDA.